Vamos a estudiar el sistema binario de forma sencilla y fácil de entender para todo el mundo.
Actualmente la mayoría de las personas utilizamos el sistema decimal (de 10 dígitos) para realizar operaciones matemáticas. Este sistema se basa en la combinación de 10 dígitos (del 0 al 9). Construimos números con 10 dígitos y por eso decimos que su base es 10.
Por ejemplo el 23, el 234, 1093 etc. Todos son dígitos del 0 al 9.
Pero hay otro sistema o lenguaje muy utilizado que es el sistema binario de numeración,
que en algunos casos, como por ejemplo en informática, se puede llamar Lenguaje Binario, debido a que es el lenguaje que usamos
para entendernos con el ordenador.
Luego también hablaremos del Lenguaje Binario.
¿Qué es el Sistema Binario?
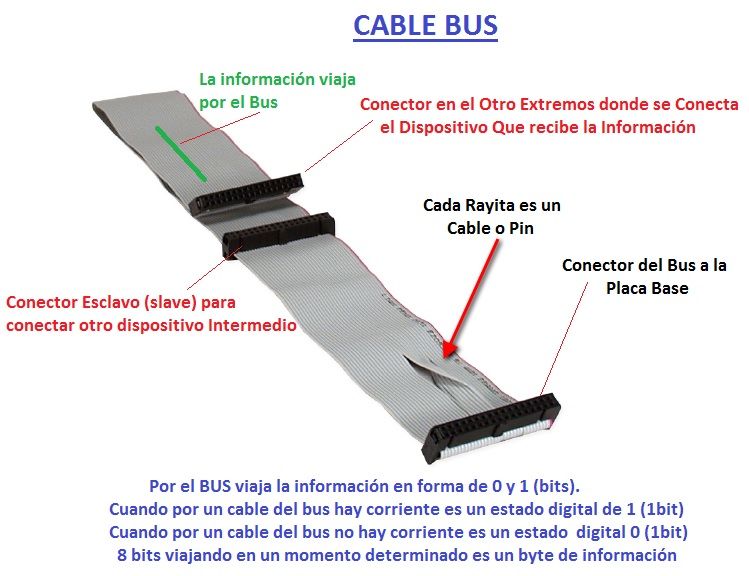
El sistema binario es un sistema de numeración en el que los números se representan utilizando las cifras 0 y 1, es decir solo 2 dígitos (bi = dos).Esto en informática y en electrónica tiene mucha importancia ya que las computadoras trabajan internamente con 2 niveles: hay o no hay de Tensión, hay o no hay corriente, pulsado o sin pulsar, etc.
Esto provoca que su sistema de numeración natural sea el binario, por ejemplo 1 para encendido y 0 para apagado.
También se utiliza en electrónica y en electricidad (encendido o apagado, activado o desactivado, etc.).
El lenguaje binario es muy utilizado en el mundo de la tecnología.

Números Binarios
Como ya dijimos, el sistema binario se basa en la representación de cantidades utilizando los números 1 y 0.Por tanto su base es 2 (número de dígitos del sistema).
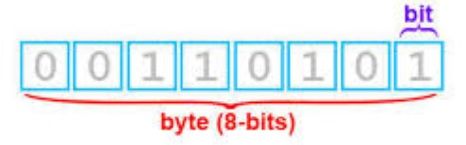
Cada dígito o número en este sistema se denomina bit (contracción de binary digit).
Por ejemplo el número en binario 1001 es un número binario de 4 bits.
Recuerda "cualquier número binario solo puede tener ceros y unos".
Los Números Binarios empezarían por el 0 (número binario más pequeño) después el 1 y ahora tendríamos que pasar al siguiente número, que ya sería de dos cifras porque no hay más números binarios de una sola cifra.
El siguiente número binario, por lo tanto, sería combinar el 1 con el 0, es decir el 10 (ya que el 0 con el 1, sería el 01 y no valdría porque sería igual que el 1), el siguiente sería el número el 11.
Ahora ya hemos hecho todas las combinaciones posibles de números binarios de 2 cifras, ya no hay más, entonces pasamos a construir los de 3 cifras.
El siguiente sería el 100, luego el 101, el 110 y el 111. Ahora de 4 cifras...
Según el orden ascendente de los números en decimal tendríamos los números binarios equivalentes a sus números en decimal :
El 0 en decimal sería el 0 en binario
El 1 en decimal sería el 1 en binario
El 2 en decimal sería el 10 en binario (recuerda solo combinaciones de 1 y 0)
El 3 en decimal sería el 11 en binario
El 4 en decimal sería el 100 en binario... Mejor mira la siguiente tabla:

Y así sucesivamente obtendríamos todos los números en orden ascendente de su valor, es decir obtendríamos el Sistema de Numeración Binario y su número equivalente en decimal.
Pero que pasaría si quisiera saber el número equivalente en binario al 23.456 en decimal.
Tranquilo, hay un método para convertir un número decimal en binario sin hacerlo uno a uno.
Decimal a Binario
Para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar).Para sacar la cifra en binario cogeremos el último cociente (siempre será 1) y todos los restos de las divisiones de abajo arriba, orden ascendente.
Ejemplo queremos convertir el número 28 a binario:
28 dividimos entre 2 : Resto 0
14 dividimos entre 2 : Resto 0
7 dividimos entre 2 : Resto 1
3 dividimos entre 2 : Resto 1 y cociente final 1
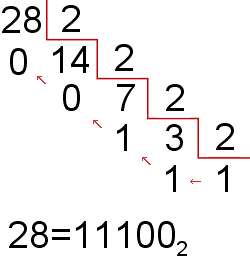
Entonces el primer número del número equivalente en binario sería el cociente último que es 1 y su resto que es también 1, la tercera cifra del equivalente sería el resto de la división anterior que es 1, el de la anterior que es 0 y el último número que cogeríamos sería el resto de la primera división que es 0.
Con todos estos número quedaría el número binario: 11100.
Conclusión el número 28 es equivalente en binario al 11.100.
Vemos como para sacar el equivalente se coge el último cociente de las operaciones y los restos que han salido en orden ascendente (de abajo arriba) 11100.
El subíndice 2 que hemos puesto al final del número en binario, es para indicar que es un número en base 2, pero no es necesario ponerlo.
Veamos otro ejemplo el número 65 pasarlo a binario.
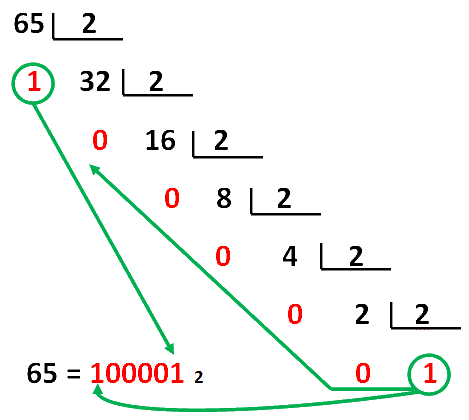
Pasar de Binario a Decimal
Pues ahora al revés.¿Que pasaría si quisiera saber cual es el número equivalente en decimal del número binario por ejemplo 1001?
Pues también hay método.
PASO 1 – Numeramos los bits de derecha a izquierda comenzando desde el 0 (muy importante desde 0 no desde 1).
PASO 2 – Ese número asignado a cada bit o cifra binaria será el exponente que le corresponde.
PASO 3 – Cada número se multiplica por 2 elevado al exponente que le corresponde asignado anteriormente.
PASO 4 - Se suman todos los productos y el resultado será el número equivalente en decimal
Vamos a verlo paso a paso con un ejemplo y gráficamente que será más sencillo de entender.
Ejemplo el número 1001 queremos saber su equivalente en decimal. Primero asignamos exponentes:
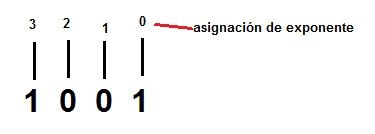
Empezamos por el primer producto, que será el del primer número binario por 2 elevado a su exponente, es decir 1 x 23 .
OJO Recuerda que cualquier número elevado a cero es 1, por ejemplo 2 elevado a 0 es = 1.
El segundo y el tercer productos serán 0 porque 0 x 22 y 0 x 21 su resultado es 0 y el último producto será 1 x 20 que será 1, luego 1 x 20 es 1 (no confundir y poner 0).
Ya estamos en el último paso que es sumar el resultado de todos estos productos:
1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 8 + 0 + 0 + 1 = 9
El equivalente en decimal del número binario 1001 es el 9.
Veamos otro ejemplo solo gráficamente para que lo entiendas definitivamente.
En este caso la asignación del exponente a cada número ya lo hacemos directamente en los productos, que es como se suele hacer normalmente.
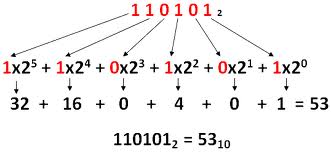
Otro ejemplo con todos los datos:
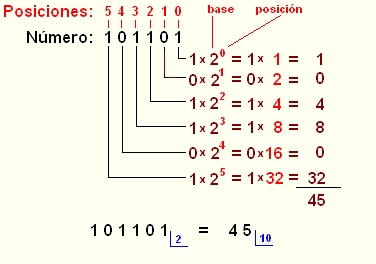
Operaciones Binarias
Las operaciones binarias que se pueden realizar con número binarios son las mismas que en cualquier otro sistema: suma, resta, multiplicación y división.Veamos algunos Ejemplos de Operaciones Binarias.
Suma de Números Binarios
Las posibles combinaciones al sumar dos bits son
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Un ejemplo con más cifras:
100110101
+ 11010101
———————————
1000001010
Operamos como en el sistema decimal: comenzamos a sumar desde la derecha, en nuestro ejemplo, 1 + 1 = 10, entonces escribimos 0 en la fila del resultado y nos llevamos 1 (este "1" se llama arrastre).
A continuación se suman los números de la siguiente columna: 0 + 0 = 0, pero como nos tenemos que sumar el 1 de la anterior suma, el resultado será 0 + 1 = 1.
Así seguimos hasta terminar todas la columnas (exactamente como en decimal).
Resta de Números Binarios
Las restas básicas 0-0, 1-0 y 1-1 son evidentes:
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = Es una resta imposible en binario porque no hay números negativos.
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 10 - 1 = 1 y me llevo 1, lo que equivale a decir en decimal, 2 - 1 = 1.
Esa unidad prestada debe devolverse, sumándola, a la posición siguiente.
Veamos algunos ejemplos:
Dos ejemplos más:
10001 11011001
-01010 -10101011
—————— ———————
00111 00101110
Multiplicación de Números Binarios
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
Por ejemplo, multipliquemos 10110 por 1001:
10110
x 1001
———————
10110
00000
00000
10110
—————————
11000110
División de Números Binarios
Igual que en el producto, la división es muy fácil de realizar, porque no son posibles en el cociente otras cifras que no sean UNOS y CEROS.
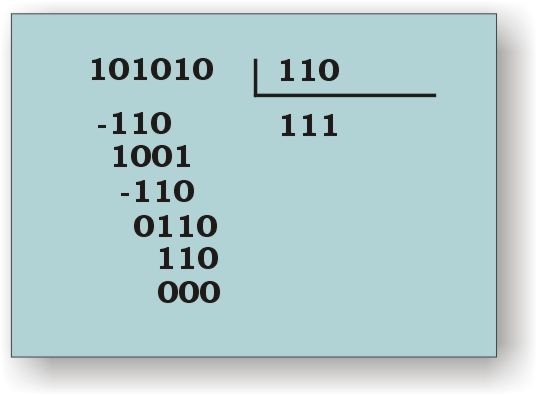
Se intenta dividir el dividendo por el divisor, empezando por tomar en ambos el mismo número de cifras (100 entre 110, en el ejemplo).
Si no puede dividirse, se intenta la división tomando un dígito más (1001 entre 100).
Si la división es posible, entonces, el divisor sólo podrá estar contenido una vez en el dividendo, es decir, la primera cifra del cociente es un UNO.
En ese caso, el resultado de multiplicar el divisor por 1 es el propio divisor. Restamos las cifras del dividendo del divisor y bajamos la cifra siguiente.
El procedimiento de división continúa del mismo modo que en el sistema decimal.
Lenguaje Binario
La misma lógica que se utiliza para representar los números se puede utilizar para representar texto.
Lo que necesitamos es un esquema de codificación, es decir, un código que nos haga equivalencias entre un número binario y una letra del abecedario.
Necesitamos un número binario por cada letra del alfabeto.
Por ejemplo, en informática, cada tecla del teclado (números, letras, signos, etc.) hay un número en binario que es su equivalente. Luego veremos muchos más.
Un ejemplo real: 0100 0001 es el número binario que representa la letra A.
En binario ese número es equivalente a la letra A.
Varios códigos estándar para convertir texto en binario se han desarrollado a lo largo de los años, incluyendo ASCII y Unicode, los más famosos y utilizados.
El Código Estándar Americano para el Intercambio de Información (ASCII) fue desarrollado a partir de los códigos telegráficos, pero luego fue adaptado para representar texto en código binario en los años 1960 y 1970.
La versión original de ASCII utiliza 8 bits (recuerda cada número binario es un bit) para representar cada letra o carácter, con un total de 128 caracteres diferentes.
Cuando hablamos de caracteres nos referimos tanto a letras, como a números, como a signos ($, /, etc.).
Este es uno de los códigos o lenguaje binario para representar texto mediante números binarios que más se utilizó durante mucho tiempo.
Mientras ASCII se encuentra todavía en uso hoy en día, el estándar actual para la codificación de texto es Unicode.
El principio fundamental de Unicode es muy parecido a ASCII, pero Unicode contiene más de 110.000 caracteres, cubriendo la mayor parte de las lenguas impresas del mundo.
La relativamente simple versión de 8 bits de Unicode (referido como UTF-8) es casi idéntica a ASCII, pero las versiones de 16 y 32 bits (referido como UTF-16 y UTF-32) le permiten representar casi cualquier tipo de lenguaje impreso.
A continuación puedes ver una tabla con el código para representar letras y caracteres en ASCII y en UNICODE de 16 bits.
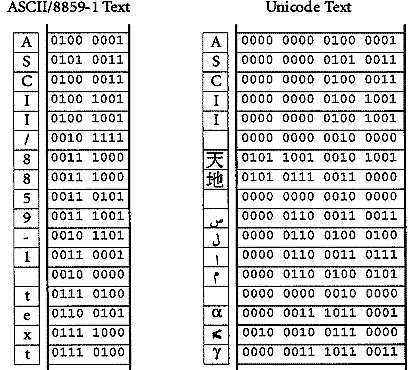
Como ves en ASCII cada letra se representa por un número binario de 8 números y UNICODE por 16.
Así podemos construir un lenguaje binario donde cada letra se representa por un número binario.
Estos códigos son lo que se llama en informática, el código máquina, y es el utilizado por todos los ordenadores para entenderse con las personas.
Los programadores, escriben sus programas en un lenguaje de programación, que posteriormente tienen que convertirlo a código máquina para que lo entienda el ordenador.
Si quieres saber más sobre este te recomendamos el siguiente enlace: Lenguajes de Programación.

Según el Diccionario Enciclopédico de Oxford, una entrada aritmética binaria apareció por primera vez en Inglés en 1796 en A Mathematical y Diccionario filosófico.
A Gottfried Leibniz, se le atribuye la invención del sistema de numeración binario en 1679 y estaba basado en las antiguas figuras chinas de Fu Xi.
Aunque las personas de la remota isla de Mangareva utilizaban un tipo de sistema binario mucho antes para las transacciones comerciales, dada la lejanía de Leibniz a esta isla, es probable que se acercara al código binario de forma independiente.
En 1605, Francis Bacon discutió un sistema por el cual las letras del alfabeto podrían reducirse a secuencias de dígitos binarios, que luego podría ser codificada como variaciones apenas visibles en la fuente en cualquier texto aleatorio.
Fue el primer lenguaje binario utilizado.
Otro matemático y filósofo con el nombre de George Boole publicó un artículo en 1847 llamado "El análisis matemático de la lógica" que describe un sistema algebraico de la lógica, ahora conocido como el álgebra de Boole.
El Sistema de Boole se basó en números binarios, dando un 0 o un 1, el enfoque de encendido y apagado, que consistía en las tres operaciones más básicas: AND, OR y NOT.
Hoy en día es el utilizado en Electrónica Digital.
Este sistema no fue puesto en uso hasta que un estudiante graduado de Massachusetts Institute of tecnología con el nombre de Claude Shannon se dio cuenta de que el álgebra de Boole, que estaba aprendiendo, era similar a un circuito eléctrico.
Shannon escribió su tesis en 1937, aplicando sus descubrimientos.
La tesis de Shannon se convirtió en un punto de partida para el uso del código binario en las aplicaciones prácticas, tales como computadoras, circuitos eléctricos, y muchas más.
Para acabar un video muy curioso que habla del sistema binario y los números binarios: